Narrator: You might go to a foreign land and look around and think, oh dear, everything is so very different. Do I have anything in common with this place? Or the people? But give it a few minutes and you’d find out that you have so much in common, that you’re virtually the same!
There’s a fraction. Just arrived… And oh. Look who’s here. It’s 0.5. Or point five to his mates. Oh. A half looks unsure. Looks nervous.And oh dear. Look who else has popped in? 50%. He is an intimidating fellow.
But guess what? Deep down, they’re all the same.
Narrator: Fractions, Decimals and Percentages are different ways to express values that are less than a whole. No. Don’t turn that music down. I like it. You’ll learn to change fractions, decimals and percentages into one another, but before you do that, you’ve got to get to know what they are! It’s time to – pump that music up! – and it’s time to ~
V.O: Kick Sum Maths!
Narrator: FRACTIONS, DECIMALS AND PERCENTAGES
Narrator: Have a look at this fraction. We say the top line is a numerator and the bottom line is the denominator. So the denominator is 2 and the numerator is 1. It’s telling us it’s one of two bits.
But this fraction, a half could also be 2/4ths, 4/8ths, 33/66ths or any other fraction that’s equivalent to a half.
Narrator: For fractions, we can change the denominators and numerators as long as they stay in proportion.What’s proportion? Well, 1/2 is equal to 2/4 or 3/6 or 4/8.
In each of these, the numerators and denominators are getting bigger, but each by the same factor.
Now, let’s look at the percentage. It’s 50 percent. Which means it’s 50 out of 100. As a percentage, the denominator stays at a 100. It’s what makes a percentage a percentage, it’s something out of a 100
Narrator: Now, what about decimals? Here's 0.5. This digit is in the ones column. Here's the decimal point. This digit is in the tenths column. Tenths are parts out of ten. Half of ten is 5, so 0.5 is the same as 1/2.
But check out this move. There can be more than one decimal place. If the first one is tenths, then the second decimal place is a hundredth, and the third is a thousandth! And do you know how long this decimal can stretch for? Go on, show ‘em!
Narrator: Actually decimal places can go on forever. But who’s got time to count all that lot? Not me. Don’t worry. Usually 2 or 3 decimal places are enough. Now that you know the difference between fractions, decimals and percentages and you know that ½ is the same as 0.5 or 50%, you can do some fancy moves yourself. Do you want to see my fancy moves?
Phresh!!!
Interviewer: So your team got beaten, you must be pretty upset?
Manager: Yes I’m disappointed, but not with the lads. They gave a 110% effort today
Interviewer: I’m sorry what was that?
Manager: I’m disappointed but-
Interviewer: No not that. The other thing you said?
Manager: The lads gave 110%.
Interviewer: How much??
Manager: 110%.
Interviewer: That’s impossible. Sure if you had 5 biscuits and someone gave you and 6 more biscuits you’d be increase the number of biscuits you had by 120%. but you can’t give more than 100% effort because 100% effort means giving all your effort.
Manager: Well my boys did. They played their socks off-
Interviewer: Look, here would be zero effort, the minimum, and here would be maximum effort, which is 100%. Are you seriously trying to tell our viewers that your players put more of an effort into the game than it was possible to put in to the game?
Manager: It’s just a saying.
Interviewer: It’s nonsense that’s what it is. Just give me a straight answer. How much effort did your players give on the park today?
Manager: One hundred and-
Interviewer: No!! How much effort did they really give? Need I remind you that the score was 50-3 and that the opposition actually did give 100% which would suggest that your team gave?
Manager: My team gave… 6% effort?
Interviewer Barry Coleslaw, thank you!
Video summary
In this clip we look at the structure of fractions, decimals and percentages and how they are different ways of representing quantities or proportions.
We see how a fraction is composed, the meaning of “percentage” as an amount “out of 100”, and place values in a decimal.
We also see a connection between fractions, decimals and percentages.
The end sketch looks at the “giving 110%” platitude often associated with sport commentary and analyses why it is incorrect.
This clip is from the series Kick Sum Maths.
Teacher Notes
This clip could be used to consolidate the meaning of fractions. It can also be used to illustrate the meaning of percentage and place value for decimals.
The end sketch could stimulate discussion of when more than 100% makes sense and when it doesn't. Clearly, this clip also leads on to Decimal Dance Off 2.
These clips could be used for teaching Maths at KS2 or at a beginner level in England, Wales and Northern Ireland and 1st and 2nd Level in Scotland.
Decimal Dance Off 2 video
The connection between fractions, x decimals and percentages and how to convert between them are explored through a 'Decimal Dance Off'.
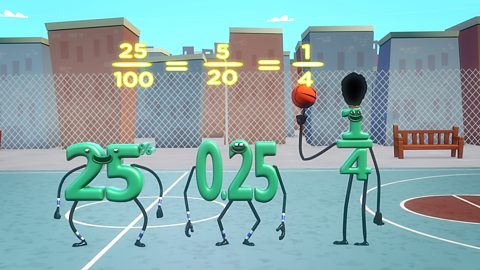
As The Crow Flies. video
A demonstration of how to calculate the perimeter and area of simple and compound shapes with the help of the crow and Detective Stinker.

Geometry Rules OK. video
Introducing geometry, angles and shapes through a spoof house building show and an animation game show.

Let's Have Some Order. video
An explanation of why using the correct order in mathematical calculations is important.

Pie And Pie Again. video
An introduction to pie charts and how they show relative proportions.

Prime Suspects 1. video
Introducing prime numbers, composite numbers and factors in a sketch show featuring puppet Detective L Stinker and his animated friends.

Prime Suspects 2. video
Decompose numbers into prime factors. End sketches look at primes and simple sequences.

Scale And Polish. video
A look at the meaning of scale factors and how they allow us to represent large objects in two and three dimensions.

Scale And Polish. video
A look at the meaning of scale factors and how they allow us to represent large objects in two and three dimensions.

X Marks The Thought. video
An introduction to using algebra to solve simple equations by using inverse operations.
