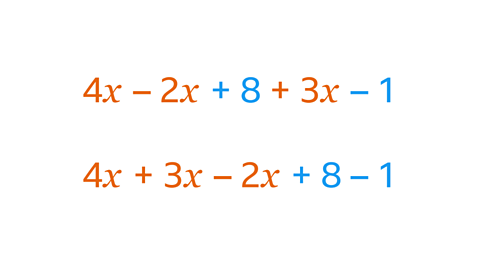Key points
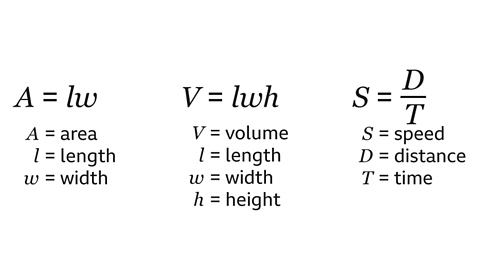
- Understanding algebraic notation and the order of operations (BIDMAS) will help in using formulae successfully.
- A formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae. is a rule that links variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚 and may be expressed in words or written ‘algebraically’, using mathematical symbols.
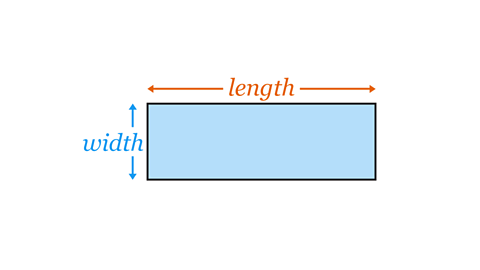
- Formulae connect variables in a mathematical relationship. For example, the area, length, and width of a rectangle are connected by a formula. When two of the variables are given, the third can be worked out using the formula.
- Numbers are substituteIn algebra substitute means to replace a letter (or variable) with a number. into a formula to find the value of the subject.
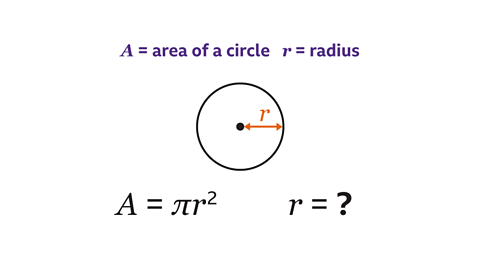
- A formula may be rearrange (a formula)Change the subject of a formula. The formula for the area of a circle (A = πr²) can be rearranged to change the subject, in this case to make the subject the radius r =√(A/π) to change the subject. By manipulating the algebra, a different variable becomes the subject (of a formula)The formula for the area of a circle is A = πr² The area A is the subject of the formula. The subject can be changed if the formula is rearranged. of the formula.
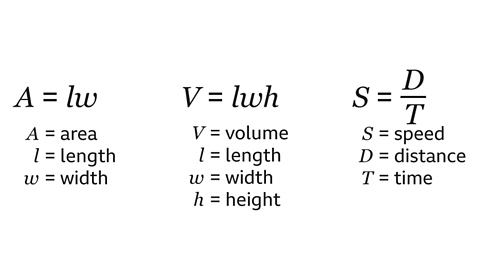
Using formulae given in words
A formula given in words gives the instructions needed to work something out.
To use a written formula:
- Substitute a given value for the variable.
- Follow each step in the formula instructions to work out the subject of the formula.
Examples
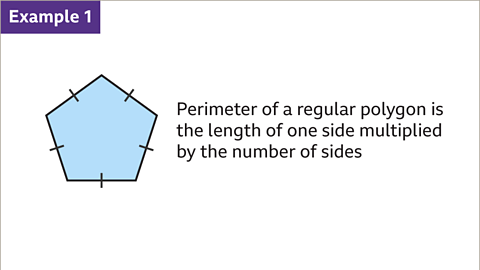
Image caption, The perimeter of a regular polygon is the length of one side multiplied by the number of sides. Use this formula to find the perimeter of a regular pentagon with a side length of 12 cm.
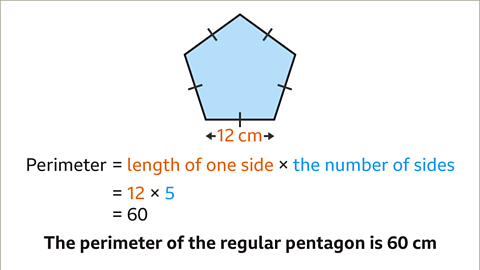
Image caption, Substitute the given values for the length of one side (12) and the number of sides (5). Follow the formula instruction (multiply 12 by 5), 12 × 5 is 60. The perimeter of the regular pentagon is 60 cm.

Image caption, A plumber places an advert with a formula for the charges made. £35 per hour plus a call out charge of £60. Find the total cost of a call that takes three hours to complete.

Image caption, The plumber charges £35 per hour. For 1 hour this charge is 1 × 35, for 2 hours 2 × 35, and for 3 hours 3 × 35 and so on. The total cost will be more because the call out charge must be included.

Image caption, The total cost is made up of the cost of the time taken and the call out charge. The call out charge is £60, 60 is added to the cost of the number of hours the job takes.

Image caption, Follow each step in the formula instructions, multiply the cost per hour (35) by the number of hours taken (3) and then add on the call out charge (60). The total cost of the three hour call is £165

Image caption, The time to cook a pie is given by a formula that depends on its mass. Find the cooking time for a 1000g pie.

Image caption, Substitute the mass of the pie (1000) into the formula. Follow each step in the formula. Divide the mass of the pie (1000) by 500, this gives how many 500g of pie there is. Then multiply by 25. Finally add 15 to get the total cooking time.

Image caption, 1000 ÷ 500 = 2. There are two lots of 500g of pie, 25 minutes per 500g, so 25 × 2, then add on the extra 15. The total cooking time is 65 minutes.
1 of 9
Question
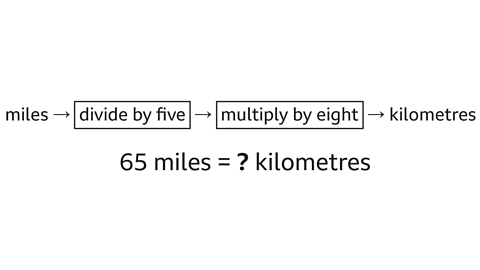
The formula for converting a distance in miles to a distance in kilometres is to divide by five and then multiply by eight.
Use the formula to convert 65 miles to kilometres.
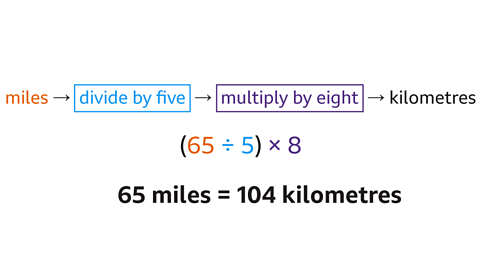
Substitute the given value for the distance in miles (65) and follow the formula instructions.
Divide 65 by 5, then multiply by eight (65 ÷ 5 × 8).
65 miles is 104 kilometres.
Constructing formulae from words
A formula written in words can be written using mathematical symbols.
- A letter or symbol is assigned to each variable.
- The formula always starts with the subject variable followed by the equals symbol.
- The expression after the equals symbol gives each instruction in the written formula using correct algebraic notation. The variables must be defined.
Confidence in writing mathematical formulae from a worded formula relies on a good understanding of algebraic notation.
Examples

Image caption, Construct an algebraic formula for speed.

Image caption, A letter or symbol is assigned to each variable. S represents the speed. D represents the distance travelled. T represents the time taken. The formula always starts with the subject variable followed by the equals symbol. The subject of this formula is the speed. The formula starts with S =

Image caption, The expression after the equals symbol gives each instruction in the written formula using correct algebraic notation. The distance travelled (D) is divided by the time taken (T). The formula must be written using correct algebraic notation. S = ᴰ/ᴛ

Image caption, The time taken to cook a pie depends on its mass. Cook for 25 minutes per 500g plus an extra 15 minutes.

Image caption, A letter or symbol is assigned to the subject and each variable. T represents the time to cook the pie. M represents the mass of the pie in grams. The formula always starts with the subject variable followed by the equals symbol. The subject of this formula is the time. The formula starts with T =

Image caption, Each 500 g of pie is cooked for 25 minutes. To find out how many lots of 500g there are, the mass (M) is divided by 500, this is M/500. This amount is multiplied by 25. The extra 15 minutes is then added on. The formula is T = M/500 × 25 + 15. The formula can be simplified.

Image caption, Dividing the mass by 500 and then multiplying by 25 can be simplified to the mass divided by 20 because 25/500 is equivalent to 1/20. (500 and 25 are both divided by 25). The formula simplifies to T = M/20 + 15
1 of 7
Question
To find the perimeter of a rectangle, add a length and a width and then double the result.
Write this formula in algebra.
A letter or symbol is assigned to each variable.
𝑷 represents the perimeter. 𝒍 represents the length. 𝒘 represents the width.
The formula starts with 𝑷 =
The expression after the equals symbol gives each instruction in the written formula. The length and width of the rectangle are added, then the result of this is doubled (multiplied by two).
The expression is written using correct the algebraic notation.
The formula is 𝑷 = 2(𝒍+𝒘).
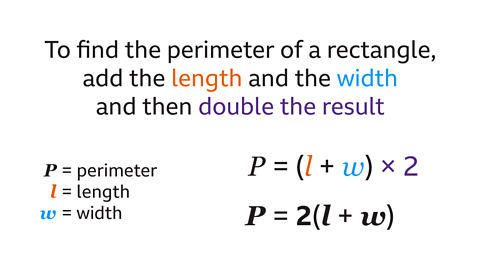
Substitution using formulae
A formulaA fact, rule, or principle that is expressed in words or in mathematical symbols. Plural: formulae. is a rule written using mathematical symbols. Values are substituteIn algebra substitute means to replace a letter (or variable) with a number. into a formula to work something out.
To use an algebraic formula:
- Substitute a given value or values for the variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚 or variables.
- Follow each step in the formula instructions to work out the subject.
When the formula involves multiple steps, it is essential that the correct order of operations is followed to ensure that the calculation is accurate.
Examples

Image caption, Formulae are rules written using mathematical symbols.
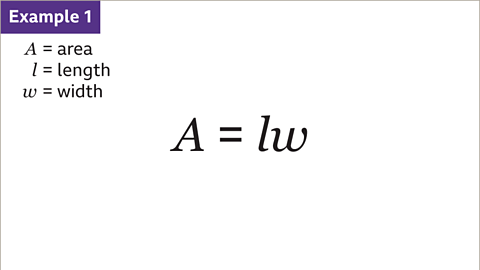
Image caption, Use the formula to work out the area (𝑨) of a rectangle with a length (𝒍) of 15 cm and a width (𝒘) of 3 cm.

Image caption, The length of the rectangle is 15 cm. The width of the rectangle is 3 cm. Substitute the given value (15) for the length, (𝒍), and the given value (3) for the width, (𝒘). Follow the formula instruction. The length is multiplied by the width to work out the area of the rectangle.
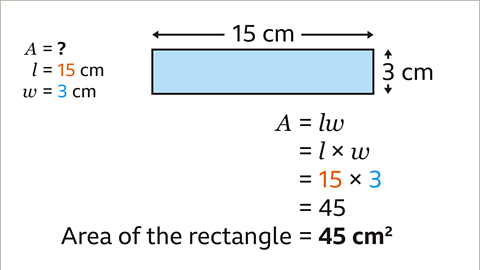
Image caption, 15 × 3 = 45. The area of the rectangle is 45 cm².
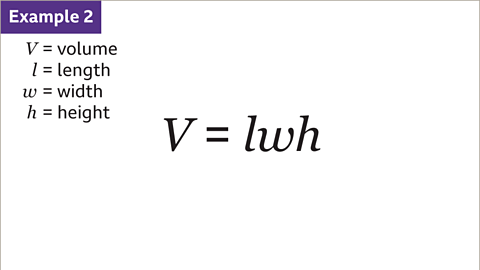
Image caption, Use the formula to work out the volume, (𝑽), of a cuboid with a length, (𝒍), of 10 cm, a width, (𝒘), of 4 cm and a height, (𝒉), of 7 cm.
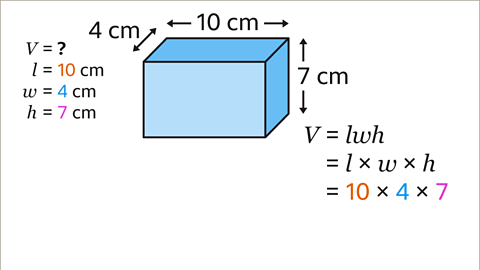
Image caption, The length, (𝒍), of the cuboid is 10 cm, the width, (𝒘), is 4 cm and the height, (𝒉), is 7 cm. Substitute these values into the formula. Follow the formula instruction. The length, width and height of the cuboid are multiplied together to find the volume of the cuboid.

Image caption, 10 × 4 × 7 = 280. The volume of the cuboid is 280 cm³
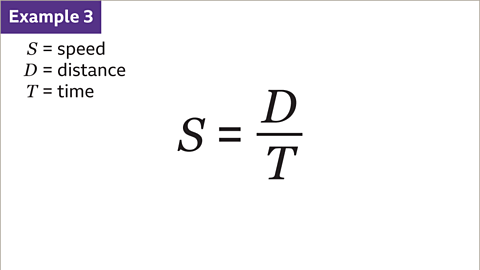
Image caption, Use the formula to find the speed (𝑺) of an object that travels 186 metres distance, (𝑫) in 5 seconds time, (𝑻).

Image caption, The distance, 𝑫, is 186 metres. The time, 𝑻, is 5 seconds. Substitute the given values, 186 for 𝑫 and 5 for 𝑻. Follow the formula instruction. The distance (186) is divided by the time (5) to work out the speed.

Image caption, 186 ÷ 5 = 37۰2. The speed of the object is 37۰2 metres per second.
1 of 10
Question
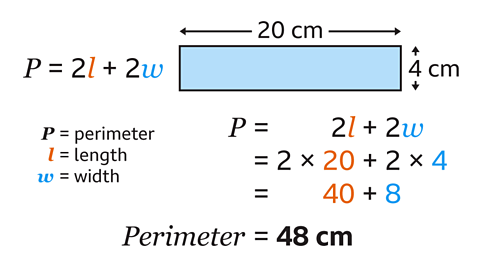
Use the formula to work out the perimeter of the rectangle.
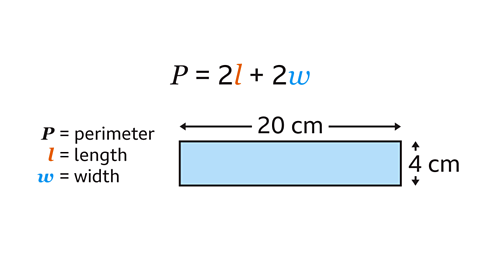
Substitute the given values of length (20) and width (4) for the variables (𝒍 and 𝒘) in the formula.
Follow each step in the formula instructions. Multiply the length by two, multiply the width by two and add the results together.
2 × 20 + 2 × 4 = 48
The perimeter of the rectangle is 48 cm.
Practise writing and constructing formulae
Quiz
Practise writing and constructing formulae with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

Formulae are used often in real life, for example when calculating the amount of paint to decorate a room, the size of a radiator to heat a room or the amount of ribbon needed to add to a wrapped gift.
A decorator buys the amount of paint needed to complete a job. A litre of emulsion paint will cover approximately 12 square metres (12 m² ).
To work out how many litres of paint are required, the formula is:
𝑳 = \(\frac{(𝒉 × 𝒘 × 𝒄 )}{12}\)
𝑳 = number of litres of paint needed
𝒉 = height of walls
𝒘 = total width of all walls
𝒄 = number of coats of paint required
For a room that will need three coats of paint with a wall height of 2۰8 metres and a total wall width of 14 metres, the calculation will be \(\frac{(2۰8×14×3)}{12}\)
The paint required is 9۰8 litres.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from BBC Bitesize.

More on Expressions and formulae
Find out more by working through a topic
- count8 of 8
- count1 of 8
- count2 of 8
- count3 of 8