This module builds on M6 Probability.
Number of outcomes
To calculate the probability of an event, the total number of possible outcomes is often required. For simple situations, making a list or completing a sample space diagram is enough but in more complex situations the product rule for counting is needed.
The rule is:
To find the total number of outcomes for two or more events, multiply the number of outcomes for each event together.
Example
A restaurant menu offers 4 starters, 7 main courses and 3 different desserts. How many different three-course meals can be selected from the menu?
Solution
Multiplying together the number of choices for each course gives
\(4 \times 7 \times 3 = 84 \)
Eighty-four different three-course meals can be selected.
Question
Miley is choosing a new 4-digit pin number. Her friend says that if you allow zeros and repeated digits, there are 40 different 4-digit numbers available (0 to 9 in each of 4 slots so \(4 \times 10 = 40\)).
Miley says that there are a lot more than that.
Is Miley right and if so, how many different 4-digit numbers are there?
Miley is right. Using the product rule for counting, there are \(10 \times 10 \times 10 \times 10 = 10000\).
Mutually exclusive events
Two events are mutually exclusive if they cannot occur at the same time.
Example
Selecting an Ace
Selecting a Jack
The 'OR' rule: the addition rule
If A and B are mutually exclusive events.
- \(P(\text{A or B}) = P(A) + P(B)\)
Example
A bag of sweets contains 7 toffees, 5 gummies and 6 caramels.
A sweet is selected at random. What is the probability of a toffee or a caramel being selected?
Solution
The events 'choosing a toffee' and 'choosing a caramel' are mutually exclusive - they cannot happen at the same time when just one sweet is being selected.
Use the addition rule (the 'OR' rule):
\(P(\text{A or B}) = P(A) + P(B)\)
\(P(\text{toffee}) = \frac{7}{18}\) – there are 18 sweets altogether, and 7 are toffee
\(P(\text{caramel}) = \frac{6}{18}\)
\(P(\text{toffee OR caramel}) = \frac{7}{18} + \frac{6}{18} = \frac{13}{18}\)
Question
Lisa and Rosa are playing a game with animal cards. Lisa has 4 lion cards, 2 giraffe cards and 1 tiger card. Rosa takes one of Lisa's cards without looking at the pictures.
What is the probability that she takes a giraffe or a tiger card?
Answer
There are 7 cards altogether.
\(P(\text{Giraffe}) = \frac{2}{7}\)
\(P(\text{Tiger}) = \frac{1}{7}\)
Use the addition rule:
\(P(\text{A or B}) = P(A) + P(B)\)
\(P(\text{Giraffe or Tiger}) = \frac{2}{7} + \frac{1}{7} = \frac{3}{7}\)
Independent events
Two events are independent if the occurrence of one event is unaffected by the occurrence of the other.
'Tossing a coin and getting a tail' and 'rolling a dice and getting a 6' are independent events.
The 'AND' rule: the multiplication rule
If A and B are independent events
\(P(\text{A and B}) = P(A) \times P(B)\)
Example
Rory rolls a dice and tosses a coin at the same time. What is the probability that he gets tails on the coin and a 6 on the dice?
Solution
Use the multiplication Rule (the AND rule):
\(P (\text{A and B}) = P(A) \times P(B)\)
\(P(\text{tails}) = \frac{1}{2}\)
\(P(\text{six}) = \frac{1}{6}\)
\(P(\text{tails and six}) = \frac{1}{2} \times \frac{1}{6} = \frac{1}{12}\)
Question
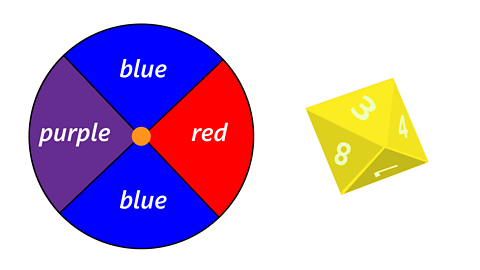
Hannah has a spinner with four equal sectors and an 8-sided dice as shown above.
She spins the spinner and rolls the dice at the same time.
What is the probability that she gets blue on the spinner and a 5 on the dice?
\(P(\text{blue}) = \frac{1}{2}\)
\(P(\text{five}) = \frac{1}{8}\)
\(P(\text{blue AND five}) = \frac{1}{2} \times \frac{1}{8} = \frac{1}{16}\)
Tree diagrams
Tree diagrams are a visual way of showing all possible outcomes of two or more events. Each branch is a possible outcome and is labelled with a probability.
Two events are independent if the probability of the first event happening has no impact on the probability of the second event happening.
For example, the probability of rolling a 6 on a dice will not affect the probability of rolling a 6 the next time. The scores on the dice are independent.
If a dice was to be rolled twice, the tree diagram would look like this:
There are four possible outcomes. To work out the probabilities of each total outcome, multiply the probabilities together.
Question
A bag contains 4 blue counters and 3 red counters. A box contains 5 blue counters and 2 red counters.
Complete the tree diagram and work out the probability of selecting two red counters.
Answer
Use the fact that probabilities add up to 1 to work out the probabilities of the missing branches.
The probability of selecting two red counters is \(\frac{3}{7} \times \frac{2}{7} = \frac{6}{49}\).
Question
Zoë plays tennis with Helen every Saturday. The probability that Zoë wins is 0.6.
Complete the probability tree and use it to find
- the probability that Zoë loses two Saturdays in a row
- the probability that Zoë loses one of the games and wins the other.
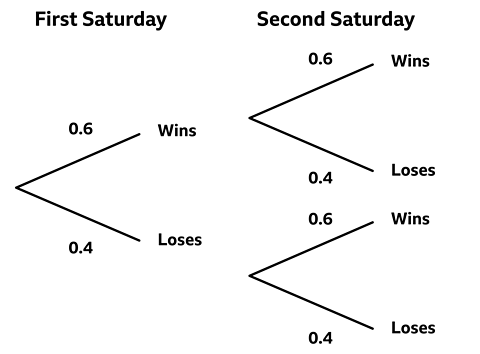
- the probability that Zoë loses two Saturdays in a row
Use the probability tree and the AND rule.
Follow the 'loses loses' branch - multiplying the probabilities.
- \(0.4 \times 0.4 = 0.16\)
The probability that Zoë loses two Saturdays in a row is 0.16.
- the probability that Zoë loses one of the games and wins the other
There are two ways that this can happen.
Zoë wins and then loses – probability = \(0.6 \times 0.4 = 0.24\)
OR
Zoë loses and then wins – probability = \(0.6 \times 0.4 = 0.24\)
Use the OR rule:
\(0.24 + 0.24 = 0.48\)
The probability that Zoë loses one of the games and wins the other = 0.48.