Key points
To add or subtract decimals, an understanding of place valueThe value of a digit that relates to its position or place in a number. Eg, in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 units. is useful.
The ability to sumThe answer to an addition calculation single digits makes this a quick way to get the total of a list of decimals.
In subtraction, regroupingRewrite a value to enable subtraction. 5 units and 2 tenths may be regrouped to 4 ones and 12 tenths. This is also known as exchanging, where, for example, a unit is exchanged for 10 tenths. may be necessary to complete the process.
How to add decimals
To add decimals:
Write the numbers in a vertical list, lining up the decimal points.
If the numbers have a different amount of digits, there may be some gaps in the columns. Fill in any gaps with a zero so that each number has the same number of decimal places.
Add a decimal point in the answer space, lined up with the others.
Start at the right, the column with the least place valueThe value of a digit that relates to its position or place in a number. Eg, in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 units.. Add the digits in the column.
- If the total is less than 10, enter the digit in the answer space.
- If the total is 10 or more, enter the units digit in the answer space for the column and carry the tens digit to the next column on the left.
- Move left to the next place value column. Add the digits in the column and add any digit that was carried to this column. Repeat the addition process in each column until the calculation is complete.
Examples

Image caption, Add 18∙42 and 5∙37. Write the larger number (18∙42) above the smaller number (5∙37) in a vertical list, lining up the decimal points. Draw an answer space with two lines. Add a decimal point in the answer space.

Image caption, Start at the column on the right, with the least place value. This calculation is in the hundredths column. Add the digits in the column (2 + 7). The total (9) is less than 10. Enter the digit (9) in the answer space for the column. Move left to the next column.
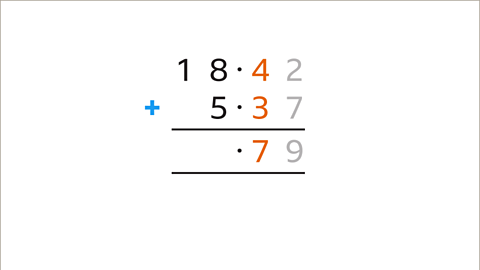
Image caption, Add the digits in the tenths column (4 + 3). The total (7) is less than 10. Enter the digit (7) in the answer space for the column. Move left to the next column.
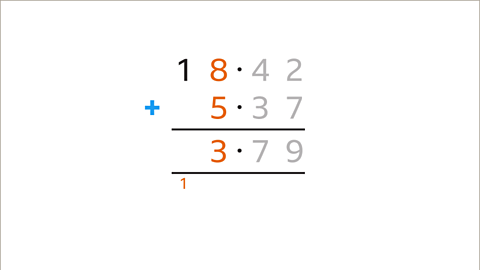
Image caption, Add the digits in the units column (8 + 5). The total (13) is greater than 10. Enter the units digit (3) in the answer space and carry the tens digit (1) to the next column. Move left to the next column.
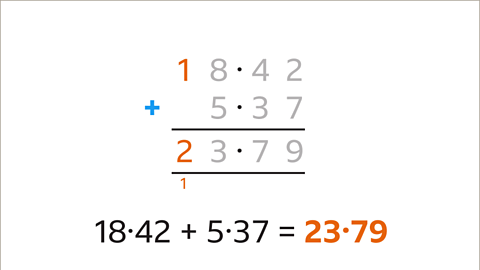
Image caption, Add the digits in the tens column (1) and add the carried digit (1). The total (2) is less than 10. Enter the digit in the answer space. The calculation is complete: 18∙42 + 5∙37 = 23∙79
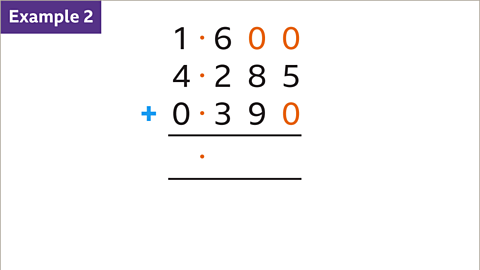
Image caption, Sum 1∙6, 4∙285 and 0∙39. Write the numbers vertically, lining up the decimal points. Fill in any gaps after the decimal point with zeros so that each number has the same number of decimal places. Draw an answer space with two lines. Add a decimal point in the answer space.

Image caption, Start at the column to the right, with the least place value. The calculation is in the thousandths column. Add the digits in the column (0 + 5 + 0). The total (5) is less than 10. Enter the digit (5) in the answer space. Move left to the next column.
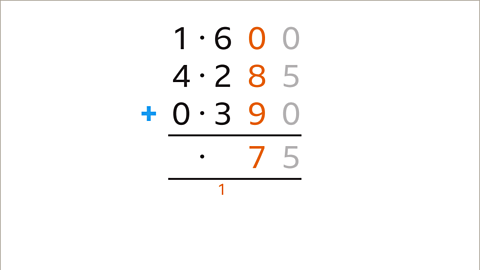
Image caption, Add the digits in the column (0 + 8 + 9). The total (17) is greater than 10. Enter the units digit (7) in the answer space and carry the tens digit (1) to the next column. Move left to the next column.
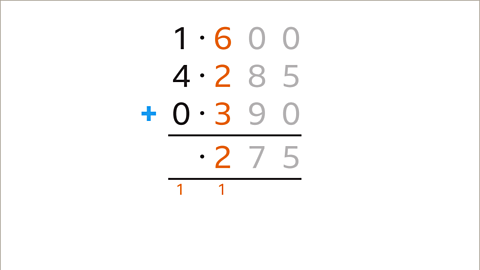
Image caption, Add the digits in the column (6 + 2 + 3) and add the carried digit (1). The total (12) is greater than 10. Enter the units digit (2) in the answer space and carry the tens digit (1) to the next column. Move left to the next column.

Image caption, Add the digits in the column (1 + 4 + 0) and add the carried digit (1). The total (6) is less than 10. Enter the digit (6) in the answer space for the column. The calculation has now been completed: 1∙6 + 4∙285 + 0∙39 = 6∙275
1 of 10
Question
Add 4∙85, 3∙6 and 7
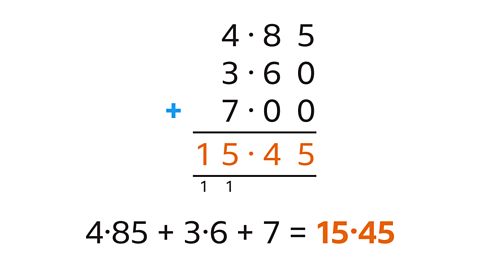
Write the numbers vertically, lining up the decimal points. The decimal point for a whole number comes after the units digit. Write in zeros so that each number has the same number of decimal places.
Start from the right, with the column with the least place value. Add the digits (5 + 0 + 0) and write the answer (5) in the answer space for the column. Move left to the next column.
Add the digits: 8 + 6 + 0. The total (14) has the units digit (4) written in the answer space and the tens digit (1) is carried to the next column. Move left to the next column.
Add the digits: 4 + 3 + 7 + the carried 1. The total is 15. Write the units digit (5) in the answer space and carry the tens digit (1) to the next column. Move left to the next column.
Add the digits (only the carried 1) and write the answer (1) in the answer space.
4∙85 + 3∙6 + 7 = 15∙45
How to subtract decimals, including regrouping
To subtract decimals:
Write the larger number above the smaller number in a vertical list, lining up the decimal points.
Column subtraction works from right to left.
Starting with the column on the right, the bottom digit is subtracted from the top digit and the answer is written in the answer space.
Move left to the next column. Complete this subtraction process for each column until the calculation is complete.
If the top digit is smaller than the bottom digit, regroup the number. Regrouping is a process where groups of 10 are borrowed from one column and given to another. It is also known as exchanging.
Look through the examples to see how to follow the regrouping process. The first example is a normal subtraction, while the second requires regrouping.
Examples
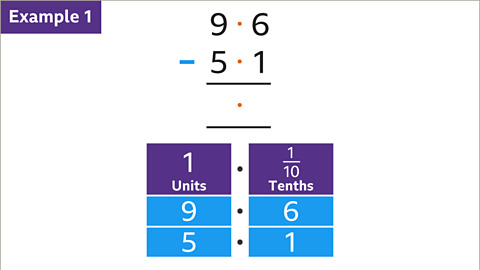
Image caption, Subtract 5∙1 from 9∙6. Write the larger number (9∙6) above the smaller number (5∙1) in a vertical list, lining up the decimal points. Draw an answer space with two lines. Add a decimal point in the answer space.
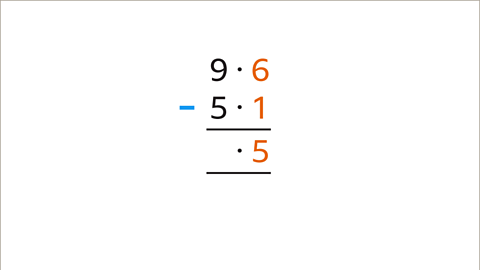
Image caption, Start at the right, the column with the least place value (tenths in this example). Subtract the bottom digit (1) from the top digit (6). The answer (5) is entered in the answer space for the column. Move left to the next place value column.

Image caption, Subtract the bottom digit (5) from the top digit (9). The answer (4) is entered in the answer space. The calculation is complete. 9∙6 - 5∙1 = 4∙5
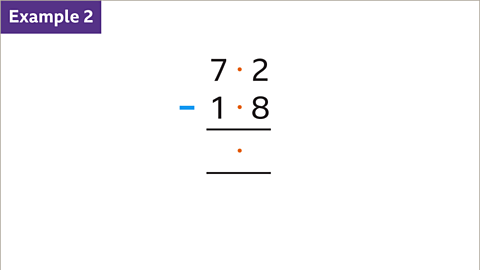
Image caption, Subtract 1∙8 from 7∙2. Write the larger number (7∙2) above the smaller number (1∙8) in a vertical list, lining up the decimal points. Draw an answer space, including a decimal point.
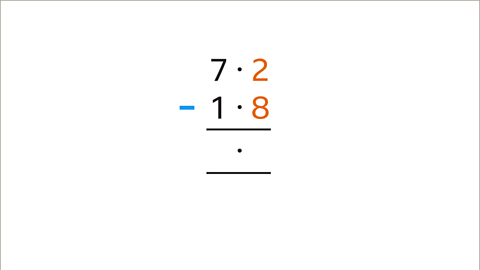
Image caption, Start at the right, the column with the least place value (tenths in this example). The top digit (2) is smaller than the bottom digit (8). 2 tenths is less than 8 tenths. Regrouping of the top number is needed.

Image caption, Regroup the top number. 7∙2 is 7 units and 2 tenths. More tenths are needed for the subtraction. Regroup so that there are 6 units and 12 tenths. Cross out the 7 and write 6. Write a 1 in front of the 2 to give 12. The subtraction can now be done.
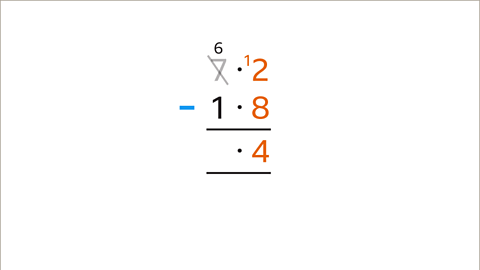
Image caption, Subtract the bottom digit (8) from the top value (12). The answer (4) is entered in the answer space for the column. Move left to the next place value column.

Image caption, Subtract the bottom digit (1) from the top digit (6). The answer (5) is entered in the answer space. The calculation is complete. 7∙2 – 1∙8 = 5∙4
1 of 8
Question
Subtract 5∙71 from 9∙04
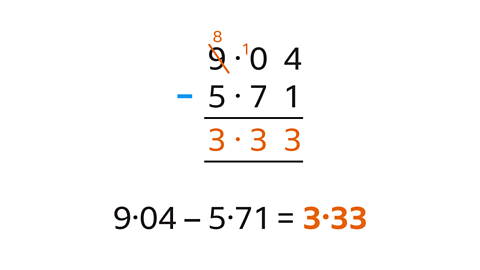
Write the larger number (9∙04) above the smaller number (5∙71) in a vertical list, lining up the decimal points.
Start from the right, the column with the least place value. Subtract the bottom digit (1) from the top digit (4). Write the answer (3) in the answer space. Move left to the next column.
The top digit is smaller than the bottom digit. Regroup the top number so that there are enough tenths for the subtraction. Subtract the bottom digit (7) from the top value (10). Write the answer (3) in the answer space. Move left to the next column.
Subtract the bottom digit (5) from the top digit (8). Write the answer (3) in the answer space. The subtraction is complete.
9∙04 – 5∙71 = 3∙33
Subtracting decimals, including regrouping across more than one column
To subtract decimals:
Write the larger number above the smaller number in a vertical list, lining up the decimal points.
Fill in any gaps after the decimal point with zeros so that each number has the same number of decimal places. Add a decimal point in the answer space, lined up with the others.
Start with the column on the right, the column with the least place valueThe value of a digit that relates to its position or place in a number. Eg, in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 units..
Subtract the bottom digit from the top digit.
When the top digit is greater or equal to the bottom digit, the answer is entered in the answer space.
When the top digit is less than the bottom digit, regroup the number to make the top digit bigger by 10. Sometimes regrouping is carried out across more than one column.
Move left to the next place value column.
Repeat the subtraction process for each column until the calculation is complete.
Examples
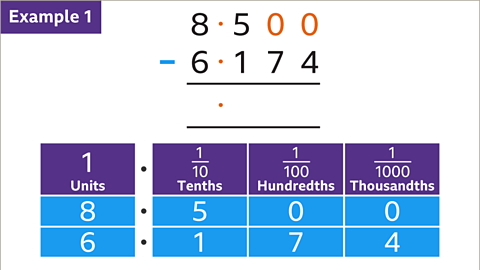
Image caption, Subtract 6∙174 from 8∙5. Write the larger number (8∙5) above the smaller number (6∙174) in a vertical list, lining up the decimal points. Fill in any gaps after the decimal point with a zero so that each number has the same number of decimal places. Add a decimal point in the answer space, lined up with the others.
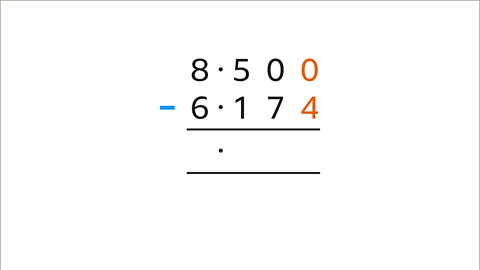
Image caption, Start at the right, the column with the least place value (thousandths in this example). The top digit (0) is smaller than the bottom digit (4). 0 thousandths is less than 4 thousandths. Regrouping of the top number is needed.
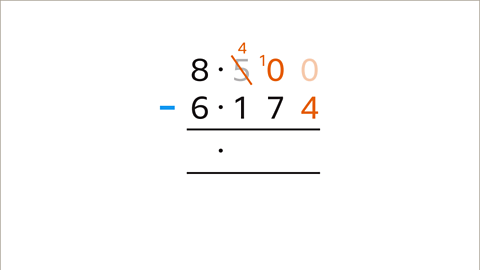
Image caption, Regroup the top number. 8∙5 is 8 units and 5 tenths. More thousandths are needed for the subtraction. Regroup so that there are 8 units and 4 tenths and 10 hundredths. Cross out the 5 and write 4. Write a 1 in front of the 0 in the hundredths column to give 10. There are still no thousandths, so the number needs to be regrouped again.

Image caption, Regroup 8 units and 4 tenths and 10 hundredths so that there are 8 units and 4 tenths and 9 hundredths and 10 thousandths. Cross out the 10 and write 9. Write a 1 in front of the 0 in the thousandths column to give 10. There are now enough thousandths for the subtraction to be processed.
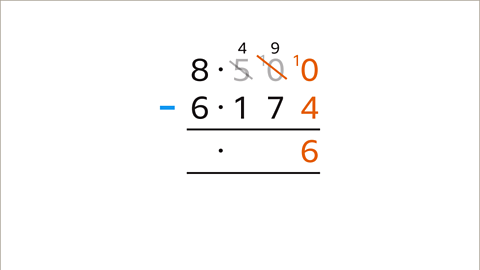
Image caption, Subtract the bottom digit (4) from the top value (10). The answer (6) is entered in the answer space. Move left to the next place value column.
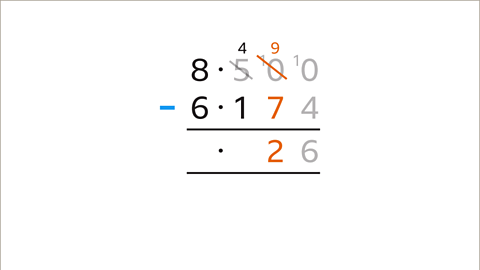
Image caption, Subtract the bottom digit (7) from the top value (9). The answer (2) is entered in the answer space. Move left to the next place value column.
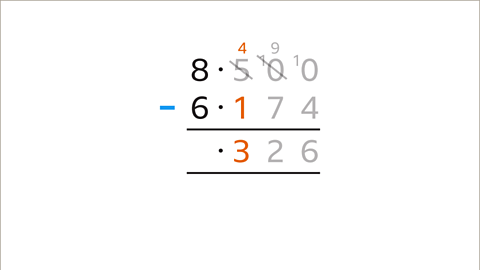
Image caption, Subtract the bottom digit (1) from the top value (4). The answer (3) is entered in the answer space. Move left to the next place value column.

Image caption, Subtract the bottom digit (6) from the top value (8). The answer (2) is entered in the answer space. The calculation is complete. 8∙5 – 6∙174 = 2∙326
1 of 8
Practise adding and subtracting decimals
Practise adding and subtracting decimals in this quiz. You might need a pen and paper for your working out.
Quiz
Real-world maths

Calculations that involve money use the addition and subtraction of decimals.
Subtraction of decimals can be used to work out how much change is needed. For example, if an item worth £17.75 is bought with a £20 note, subtraction is used to find the change required. 20 – 17.75 = 2.25. £2.25 in change is owed.
Addition of decimals can be used to total the amount of money spent on several different items. It is useful to keep track of spending when on a budget.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from BBC Bitesize.

More on Decimals
Find out more by working through a topic
- count3 of 4
- count4 of 4
- count1 of 4
