Rounding errors

Key points

Measurements (for example, time, length, and temperature) are not exact. The that they are measured to depends on the equipment that is being used and how important it is for those measurements to be precise.
Measurements can be slightly smaller or larger than recorded. The difference between the actual measurement and the recorded value is a .
Rounding errors can be expressed using two symbols to represent the lowest and highest possible values.
When rounding to the nearest one, divide the degree of accuracy by two. This provides the error interval of 0.5 either side of the whole number.
Understanding rounding decimals and also significant figures will help with rounding errors.

Why rounding errors can vary

Rounding errors can vary in size depending on the accuracy of the equipment used to measure the value.
Events can be measured to a different degree of accuracy, depending on their importance. For example, an Olympic Games 100 m race would be measured to one hundredth of a second using specialist equipment. Whereas a school sports day 100 m race might only be measured to the nearest second using a simple stopwatch.
Whilst a different type of timer is used to measure both events, the time taken can only be recorded to a set degree of accuracy. This means the actual time could be slightly different, and the would vary.
Understanding rounding decimals will help with rounding errors.

Examples

Image caption,
The winning time for the school sports day 100m race was 16 seconds (to the nearest second).
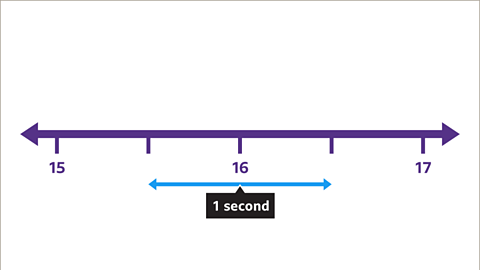
Image caption,
The time recorded is 16 seconds (to the nearest second). The actual time could be slightly quicker than 16 seconds and could be rounded up. Or the actual time could be slightly slower than 16 seconds and could be rounded down.
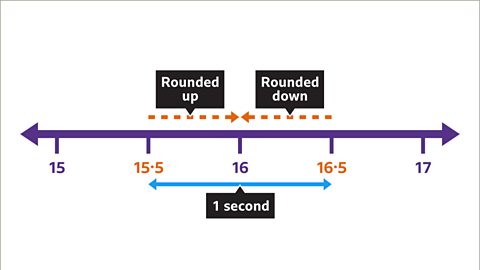
Image caption,
Times recorded at 15∙5 or above would be rounded up to 16 seconds. Time recorded below 16∙5 would be rounded down to 16 seconds.
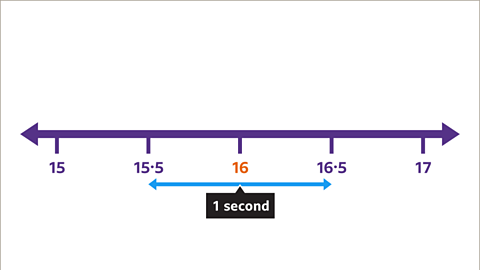
Image caption,
Any time that was recorded using the stopwatch from 15∙5 seconds up to, but not including 16∙5 seconds would be rounded to 16 seconds.
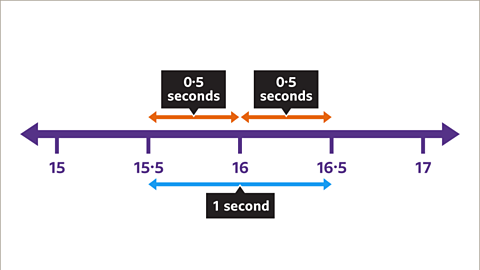
Image caption,
When rounding to the nearest one second, divide the degree of accuracy (one second) by two. 1 ÷ 2 = 0∙5. This provides the rounding error interval of 0∙5 seconds either side of the measured whole number. The rounding error for 16 seconds is 0∙5 seconds, meaning the time taken is between 15.5 and 16.5 seconds.
Image caption,
Usain Bolt broke the 100m men’s world record in 2009 (IAAF World Championships). His time was measured to one hundredth of a second at 9∙58 seconds.
Image caption,
Even at the World Championships, this time will have a rounding error. The rounding error is 0∙01 seconds, which is the decimal equivalent of one hundredth of a second.
Image caption,
Usain Bolt could have been quicker than 9∙58 seconds. He could have taken 9∙575 seconds meaning his time was rounded up. Or he might have been slightly slower and could have taken up to (but not including) 9∙585 seconds. This would mean his time was rounded down.
Image caption,
Both these 100m events were timed using different levels of accuracy. They both contain rounding errors, but to a different degree of accuracy. Timing to the nearest second has a degree of accuracy ±0∙5 seconds. Timing to the nearest one hundredth of a second has a degree of accuracy of ±0∙005 seconds.

Question

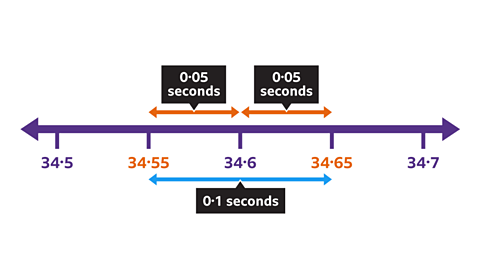
A junior swimmer completes a 50m backstroke race in 34∙6 seconds to the nearest one tenth of a second (nearest 0∙1 seconds). What would the rounding error be?

Using inequality symbols to express rounding errors

Rather than writing in full sentences, mathematicians often use symbols. The > symbol can be used instead of writing a value is greater than (or larger than).
Using two symbols can describe a value that is between two numbers eg, greater than one amount but smaller than the other.
Measured values can be slightly bigger or smaller than the actual amount. This means they can result in rounding errors. Rounding errors can be expressed using two inequality symbols to represent the lowest and highest possible values.

Examples

Skip image gallery

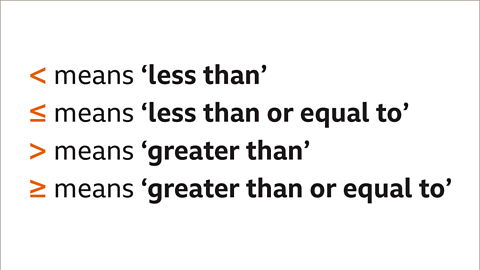
Image caption,
These 4 symbols are used regularly in maths rather than writing in full sentences.
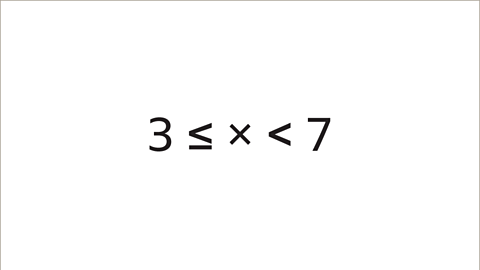
Image caption,
Two inequality symbols can be used when the value that has been measured can be within range between two numbers. This double inequality means x is greater than or equal to 3 but less than 7.
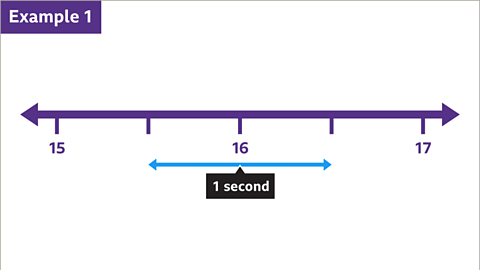
Image caption,
In the school sports day event, the time recorded for a 100m race was 16 seconds to the nearest second.
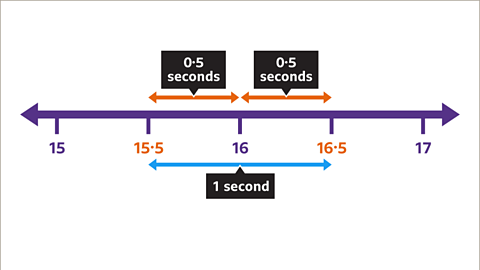
Image caption,
The time taken for the race was greater than or equal to 15∙5 seconds but less than 16∙5 seconds.
Image caption,
Using mathematical symbols this range of times could have been expressed as: 15∙5 ≤ x < 16∙5. Timing to the nearest second has a degree of accuracy ±0∙5 seconds.

Question

If ‘s’ stands for seconds, what does 120 ≤ s < 125 mean?

A The number of seconds is greater than 120 but less than 125

B The number of seconds is greater than 120 but less than or equal to 125

C The number of seconds is greater than or equal to 120 but less than or equal to 125

D The number of seconds is greater than or equal to 120 but less than 125

Practise rounding errors

Practise rounding errors in this quiz.

Quiz

Real-world maths

Woman sifting flour — Image caption,
Rounding errors are important in manufacturing because no measuring device can be 100% accurate.

Rounding errors are important to show the precision of a measurement. This is important in manufacturing because no measuring device can be 100% accurate.

Using error intervals as part of a quality assurance process allow a manufacturer to ensure their business is efficient.

A manufacturer will have a degree of tolerance (error interval) that they decide is acceptable to them.

If the weight of their product is below their lowest error interval, customers are likely to complain and potentially ask for a refund.

If the weight of the product is higher than their highest error interval, their profit margins decrease as the cost of materials are higher than necessary.

Key points

Why rounding errors can vary

Examples

Question

Using inequality symbols to express rounding errors

Examples

Question

Practise rounding errors

Quiz

Real-world maths

Game - Divided Islands

More on Rounding and estimating

Key points

Why rounding errors can vary

Examples

Question

Show moreShow less

Using inequality symbols to express rounding errors

Examples

Question

Show moreShow less

Practise rounding errors

Quiz

Real-world maths

Game - Divided Islands

More on Rounding and estimating