What are percentages?

Percentages are a way to represent a proportion of a number or a shape.
Proportion tells you how much of one thing there is in relation to the whole.
The word per cent means 'out of 100', so a percentage tells you how much of something you have out of a total of 100.
Percentages can help you to understand and compare amounts.

Quiz: Percentage problems
Test out your percentage problem-solving skills with this quiz, then read on to complete the page.
The percentage symbol
In maths, the % symbol is used to show per cent.
For example:
- 1% means 1 out of 100
- 25% means 25 out of 100, or one-quarter of something
- 50% means 50 out of 100, or half of something
- 100% means the whole thing
Percentages are used to describe parts of a whole and are used often in daily life.
What examples can you find?

People might use percentages and the percentage symbol to talk about:
- sales - where shops might offer 50% off the original price
- test scores - when someone got 100% of the answers right
- how much battery is left on a phone - when there is only 20% left
Percentage and size
The closer a percentage is to 0%, the smaller the part. The closer it is to 100%, the larger the part.
For example:
- If 10% of your class has hot food at lunch, that’s a small part of the whole class.
- If 90% of your class has cold food at lunch, that’s a large part of the whole class.
You can use tools such as grids, bar models, and part-whole models to represent percentages.
A number line can also help us see percentages.
It shows us where a percentage sits between 0% and 100%, making it easier to compare sizes.
Can you see how 10% is a much smaller part of the number line than 90%?

Percentages and fractions
Both percentages and fractions represent parts of a whole, so you can write percentages as fractions to show the same value.
Since percentages are always 'out of 100', you can write them as fractions with 100 as the denominator.
For example:
- 25% is the same as 25 out of 100, or \(\frac{25}{100}\).
- 75% is the same as 75 out of 100, or \(\frac{75}{100}\).
When you see a percentage, you can quickly turn it into a fraction by writing it over 100.
You can use the number line below to help with this.
Can you see how both the percentage and the fraction represent the same amount of a whole?

\(\frac{100}{100}\) is equivalent to 100%, which is the same as the whole.
Equivalent fractions and percentages
Let’s explore some common percentages and their equivalent fractions.
50% = \(\frac{1}{2}\)
50% means 50 out of 100. On this 100 grid, 50 of the squares are shaded.

When 50 of the squares are shaded, half of the grid is shaded. 50 is half of 100.
So, 50% is equivalent to \(\frac{1}{2}\).
25% = \(\frac{1}{4}\)
25% represents 25 out of 100. On this 100 grid, 25 of the squares are shaded.

When 25 of the squares are shaded, one-quarter of the grid is shaded. 25 is one quarter of 100.
So, 25% is equivalent to \(\frac{1}{4}\).
20% = \(\frac{1}{5}\)
20% is 20 out of 100. On this 100 grid, 20 of the squares are shaded.

When 20 of the squares are shaded, one-fifth of the grid is shaded.
20 × 5 = 100
100 ÷ 5 = 20
20% is equivalent to \(\frac{1}{5}\).
You can use these common percentages and their equivalent fractions to help you solve problems with percentages.
Example 1
Percentages can be shown on a number line.

Fred is running in a race. Roughly, what percentage of the race has Fred already run?
What percentage of the race does he have left to run?
✓ Fred has run roughly 20% of his race and he has roughly 80% of the race left to run.
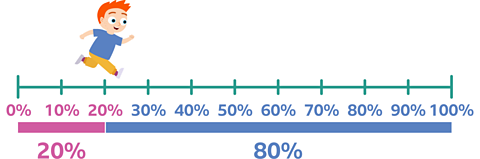
Per cent is always out of 100. So if Fred has run 20% of his race, you have to work out 100 - 20 to find out how long he has left.
100 - 20 = 80
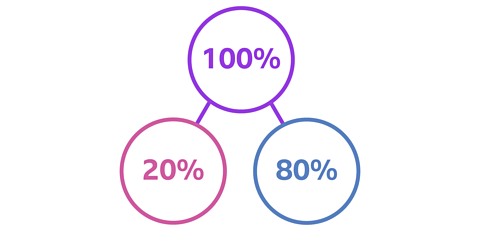
You can also show this using a part-whole model. 100% is the whole and its parts are 80 and 20.
Example 2
Rohan is reading a story. The story is 30 pages long. So far, he has read 50% of it.

How many pages has Rohan read?
✓ Rohan has read 15 pages of the story.
First, you need to find out what 50% means.
50% means 50 out of 100, or \(\frac{1}{2}\).
30 is the whole and you need to find out 50%, or \(\frac{1}{2}\), of the whole.
You need to work out \(\frac{1}{2}\) of 30.
30 ÷ 2 = 15
50% of 30 is 15.

Example 3
There are 45 people on the coach to a football match.
20% of the people on the coach are wearing hats.

How many of the 45 people on the coach are wearing hats?
✓ There are 9 people wearing hats on the coach.
First, work out how to express 20% as a fraction.
20% means 20 out of 100, which is the same as \(\frac{1}{5}\)
45 is the whole and you need to find out 20%, or \(\frac{1}{5}\), of the whole.
To find out \(\frac{1}{5}\) of 45, you have to divide 45 into 5 parts.
45 ÷ 5 = 9
9 is 20% of 45.

Play Guardians: Defenders of Mathematica to get ready for SATs. gamePlay Guardians: Defenders of Mathematica to get ready for SATs.
In this game, use the times tables and more maths skills to defeat monsters and reclaim the Kingdom.

More on Percentages
Find out more by working through a topic
- count4 of 5

- count5 of 5

- count1 of 5
