Key points
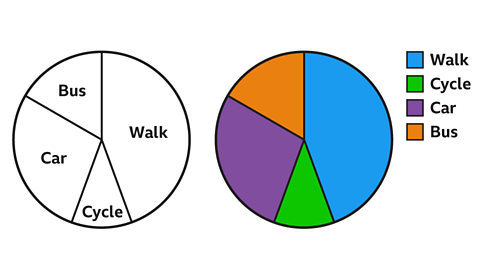
A pie chart is a type of graph used to show proportionA part-to-whole comparison. Where each part of a ratio is considered as a fraction of the whole. Eg, in the ratio 3 : 5, the first part is 3⁄8 of the whole. This is a proportion of the whole. in a sample of data. A pie chart resembles a circle which has been split into sectorA portion of a circle with a perimeter made up of two radii and an arc..
The angle of each sector is representative of the proportions of the whole data sampleThe collected data used in a survey..
If the sectors are coloured, a key should be included to explain what each colour represents.
The proportions in a pie chart may be represented as a percentageA proportion out of one hundred..
When drawing a pie chart, a protractor will be used to draw the angles accurately. Being familiar with how to use a protractor will be helpful.

Creating a pie chart
To produce a pie chart, data is required. The data often comes in the form of a table.
To create a pie chart, the size of the angles needed must be calculated.
- Add the total frequency in the table.
- Divided 360° by the total frequency.
- Multiply each frequency by this value. These are the angles for each sector.
- Construct a circle and draw a vertical line from the top to the centre.
- In a clockwise direction, use a protractor to plot each angle in turn.
- Label each sector or use a key to colour code each.
- Give your pie chart a title.
Examples
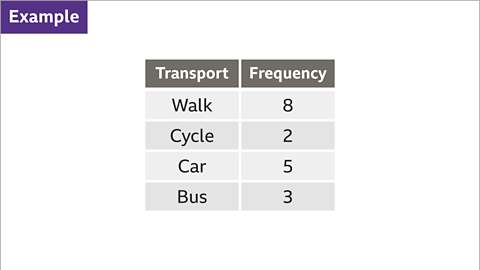
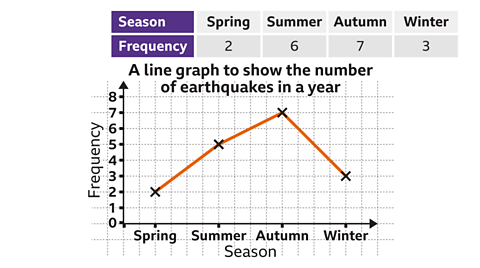
Image caption, A student asked their friends how they got to school. The table shows the results. Construct a pie chart to represent the data.
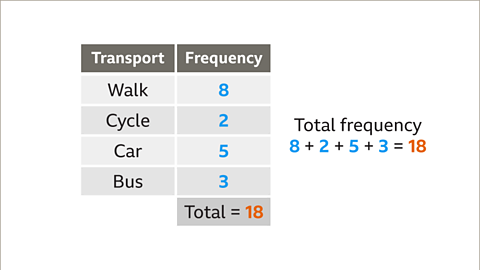
Image caption, To construct a pie chart the angles needed must be calculated. First, add the frequencies. In this table the frequencies total 18

Image caption, Divide 360° by this value. 360 ÷ 18 = 20°. This means each friend is equivalent to 20° in the pie chart.
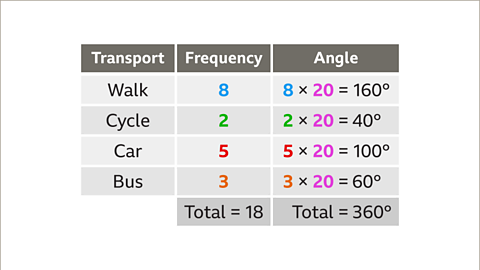
Image caption, Multiply each frequency by 20 to calculate the angles required. Walk = 8 × 20 = 160. Cycle = 2 × 20 = 40. Car = 5 × 20 = 100. Bus = 3 × 20 = 60. These angles should add up to 360°. If they do not add up to 360°, something is incorrect.
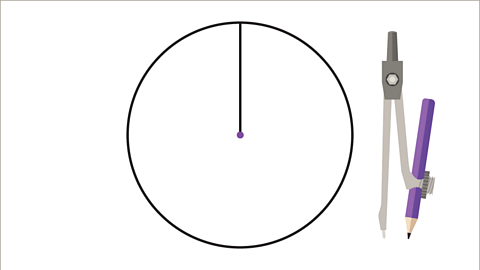
Image caption, To plot the pie chart, start by constructing a circle. Use a pair of compasses. Add a vertical line from the centre to the top of the circumference.
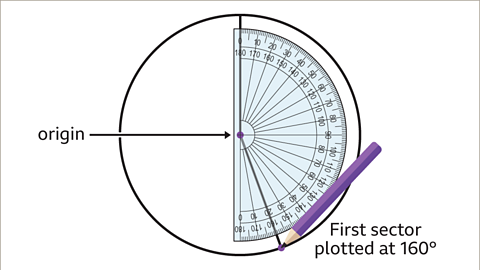
Image caption, The first sector to be drawn is to represent the friends who walk to school. This angle needs to be drawn at 160°. Position the protractor on top of the circle so that the origin is on the circle’s centre and the zero on the outer degree scale is aligned with the vertical line. Mark the angle at 160°. Remove the protractor and draw a straight line from the centre passing through this point.

Image caption, The second sector to be drawn is to represent the friends who cycle to school. This angle needs to be drawn at 40°. Rotate the protractor, keeping the origin on the centre of the circle, and with the zero on the outer degree scale now aligned with the previous line. Mark the angle at 40°. Remove the protractor and draw a straight line from the centre passing through this point.
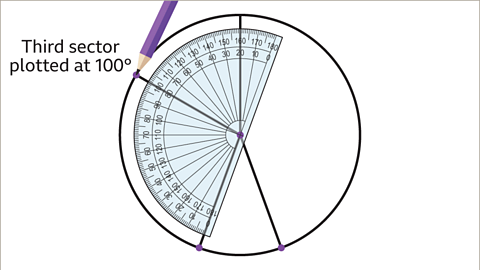
Image caption, The third sector to be drawn is to represent the friends who use a car to travel to school. This angle needs to be drawn at 100°. Again, rotate the protractor , keeping the origin on the centre of the circle and aligning the zero on the outer degree scale with the previous line. Mark the angle at 100°. Remove the protractor and draw a straight line from the centre passing through this point.
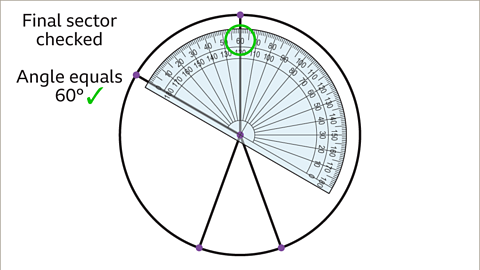
Image caption, The last sector is the angle that remains. This provides an opportunity to check how accurately the pie chart has been drawn. This angle should be 60°. This can be checked using a protractor.
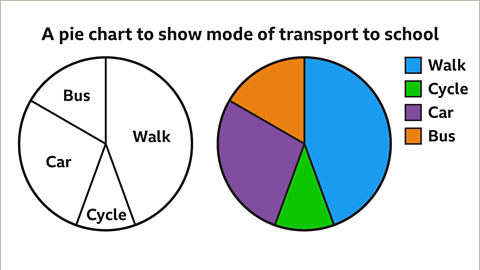
Image caption, All that is left to do is to label the pie chart and give it a title. Each sector can be labelled, or it can be colour coded with a key. An appropriate title for this example would be ‘A pie chart to show mode of transport to school’.
1 of 10
Question
A café owner recorded the type and number of drinks ordered in an hour.The table shows the results. If these were to be represented as a pie chart, what angle would be needed for each sector?
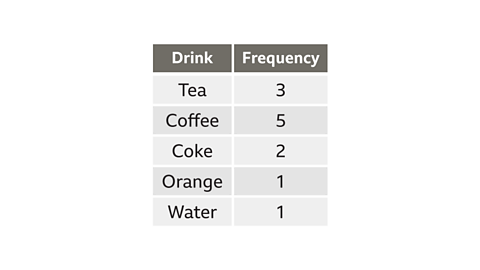
In this table the frequencies total 12
360 ÷ 12 = 30
This means each customer is equivalent to 30°.
Multiplying each drink by 30 gives:
- tea = 3 × 30 = 90
- coffee = 5 × 30 = 150
- coke = 2 × 30 = 60
- orange = 1 × 30 = 30
- water = 1 × 30 = 30

Interpreting a pie chart
It is possible to interpret a pie chart by looking at the proportions of the sectors.
The angles can be used to work out what proportion of the whole population a pie chart sector represents. These fractions would be out of 360°, the number of degrees in a full turn.
A pie chart may include the percentages of what each sector represents. These can also be used to work out proportions of the whole population.
Examples
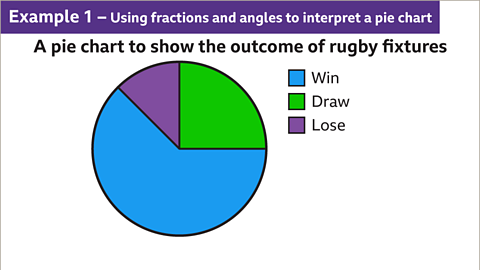
Image caption, The pie chart shows the outcome of results for a rugby team during a season.
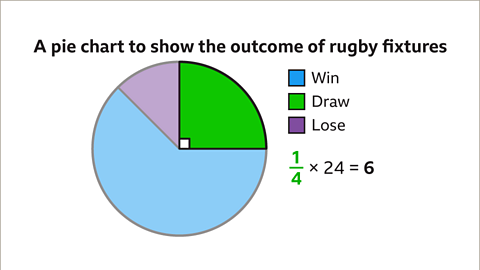
Image caption, If this pie chart represents 24 fixtures the number of each outcome can be calculated. The sector representing the fixtures that are drawn is one quarter of the fixtures. Games resulting in a draw = 1/4 × 24 = 6 games. Six games resulted in a draw.
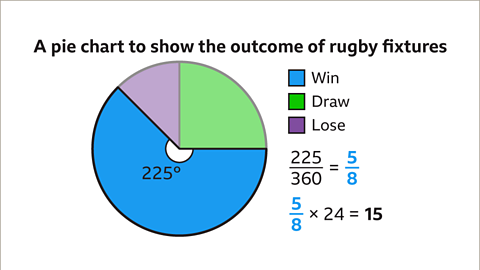
Image caption, The sector representing the fixtures that are won measures 225°. As a fraction of the whole pie chart this represents 225/360 = 5/8. Games resulting in a win = 5/8 × 24 = 15 games. Fifteen games resulted in a win.
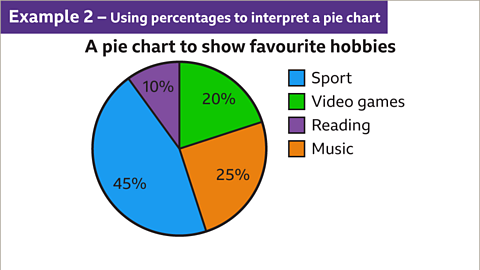
Image caption, The pie chart shows the favourite hobby of 660 pupils.

Image caption, The sector representing the pupils whose favourite hobby is playing video games is 20% of the pie chart. Number of pupils = 20% of 660 = 0.20 × 660 = 132. One hundred and thirty-two students’ favourite hobby is playing video games.
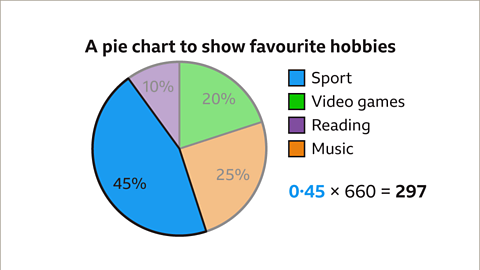
Image caption, The sector representing the pupils whose favourite hobby is playing sport is 45% of the pie chart. Number of pupils = 45% of 660 = 0.45 × 660 = 297. Two hundred and ninety-seven students’ favourite hobby is playing sport.
1 of 6
Question
The pie chart represents the types of pizza sold during one evening.If 240 pizzas were sold, how many were spicy beef & pepper?
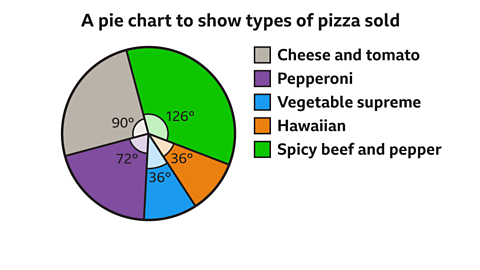
The sector representing the spicy beef and pepper pizzas measure 126°.
As a fraction of the whole pie chart, this represents \( \frac{126}{360}\) = \( \frac{7}{20}\)
Spicy beef and pepper pizzas = \( \frac{7}{20}\) × 240 = 84 pizzas.
84 spicy beef and pepper pizzas were sold.

Practise comparing and interpreting pie charts
Quiz
Practise comparing and interpreting pie charts with this quiz. You may need paper and a pen to help you.
Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from BBC Bitesize.

More on Representing data
Find out more by working through a topic
- count5 of 6

- count6 of 6

- count1 of 6

- count2 of 6