Key points

A scatter diagram or scatter graph is used to explore patterns between two sets of dataA collection of facts or observations about something. (known as 'bi-variate' data).
If there is a relationship between the two variables it is called a correlationThe relationship between two sets of data. Usually described as positive or negative..
By exploring the patterns between the variables it may be possible to draw a line of best fitA smooth line on a graph that goes through the middle of as many points as possible. Around half of any points that aren’t on the line are above it and the other half are below it. . A line of best fit generalises the trend and can be used to make predictions.

How to draw scatter diagrams and correlation
To produce a scatter diagram data is required. The data often comes in the form of a table.
To create a scatter diagram:
- Look for the smallest and largest frequencies in both variableA quantity that can take on a range of values. in your table.
- Draw a horizontal axis on your square paper or graph paper to represent one variable.
- Choose an appropriate scale for this axis and label your axis. Decide if you need to use a false originA symbol indicating a break in the scale on an axis. .
- Draw a vertical axis on your square paper or graph paper to represent the other variable.
- Choose an appropriate scale for this axis and label your axis. Decide if you need to use a false origin.
- Plot each data point carefully on the graph.
- Check you have labelled each axis correctly and give your scatter diagram a title.
Examples
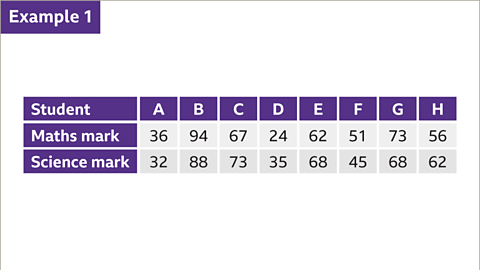
Image caption, The table shows the results of eight students' maths and science marks in an assessment. Construct a scatter graph that represents these results.
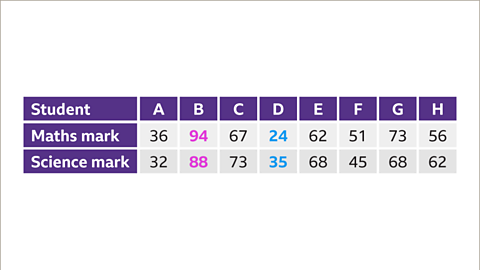
Image caption, To construct a scatter graph first identify the smallest and largest frequencies. For maths the smallest mark is 24 and the largest is 94. The horizontal axis will need to include this range. For science the smallest mark is 35 and the largest is 88. The vertical axis will need to include this range.

Image caption, Draw the horizontal axis and number it in regular intervals. In this example, the scale is increasing in increments of 20. Label the axis appropriately. Here the label on the horizontal axis is ‘Maths mark’. Draw the vertical axis and number it in regular intervals. In this example, the scale is also increasing in increments of 20. Label the axis appropriately. Here the label on the vertical axis is 'Science mark'.
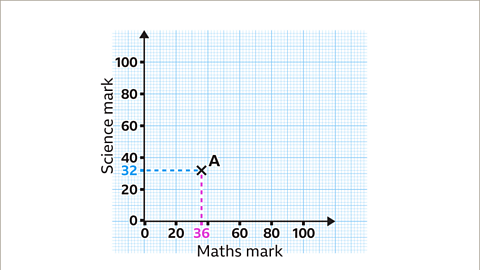
Image caption, Plot each data point in turn. For example, Student A scored a maths mark of 36 and a science mark of 32. The point needs to be plotted in line with 36 on the horizontal axis and 32 on the vertical axis.
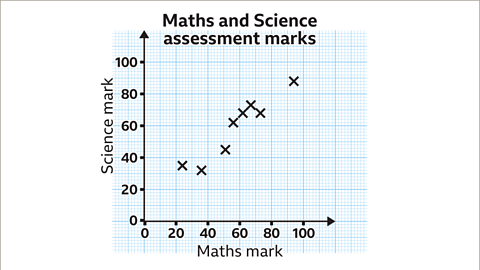
Image caption, Once all eight data points have been plotted give the graph an appropriate title, for example 'Maths and Science assessment marks'.
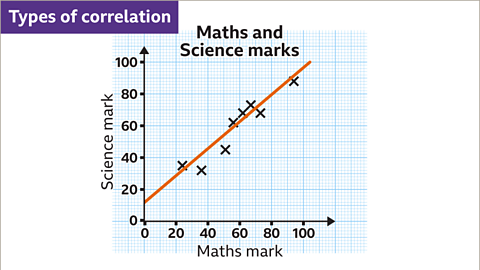
Image caption, All the data points in this graph lie approximately along a straight line. This shows there is a relationship, or correlation, between the two variables. The line has a positive gradient. This relationship is called a positive correlation. As one variable increases, the other variable increases.

Image caption, For a positive correlation, as one variable increases the other variable increases. For a negative correlation, as one variable increases the other variable decreases. A correlation is not used to describe a scatter diagram that shows no relationship between the two variables.
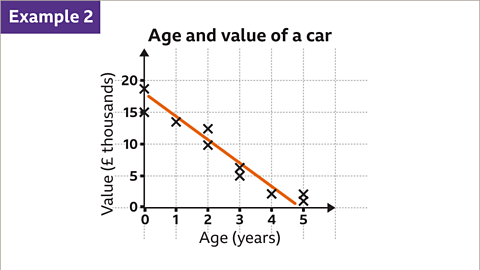
Image caption, This scatter diagram shows the age of a car and its value. This graph is an example of a negative correlation. As the age of a car increases, its value decreases.

Image caption, This scatter graph shows the distance a pupil lives from their school and their age. This graph shows there is no relationship between the two variables. There is no correlation between the age of a pupil and their distance from school.
1 of 9
Question
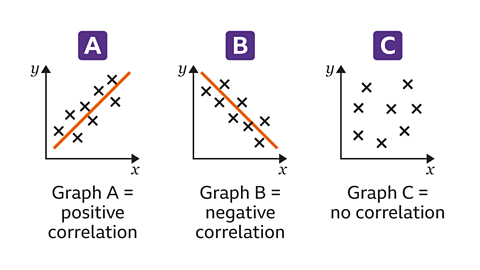
Graph A, Graph B and Graph C each demonstrate a different type of correlation.
One shows no correlation, another a positive correlation and the other a negative correlation.
Decide which correlation belongs to which graph.
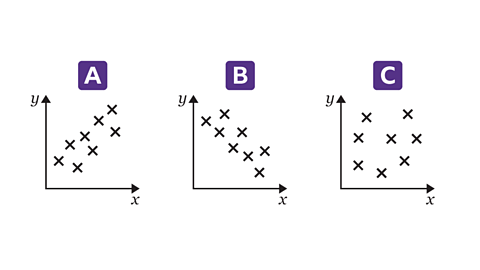
The data points in Graph A show that as one variable increases, the other variable increases. This is a positive correlation.
In Graph B, as one variable increases, the other variable decreases. This is a negative correlation.
In Graph C, the data points show no relationship between the variables, therefore there is no correlation.
How to draw and use a line of best fit
When a scatter diagram has a positive or negative correlation it is possible to draw a line of best fitA smooth line on a graph that goes through the middle of as many points as possible. Around half of any points that aren’t on the line are above it and the other half are below it. . The line of best fit should approximate the trend. The line of best fit does not have to go through the origin.
It is possible to use the line of best fit to make predictions.
If there is a data point that does not fit the trend it is called an outlier.
Examples
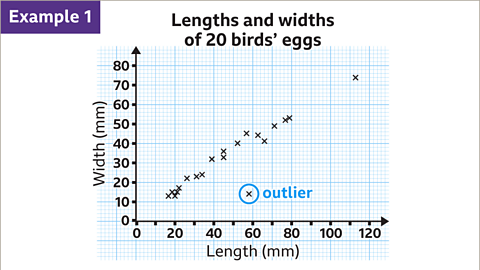
Image caption, The scatter diagram shows the relationship between the length and width of twenty birds' eggs. The horizontal and vertical scales are going up in increments of 10. Between each multiple of 10 is five subdivisions. Each subdivision is worth 2 mm. One piece of data does not match the trend. It is a long way from the rest of the data. The item of data at (58, 14) is called an outlier. Outliers need to be identified before drawing the line of best fit.
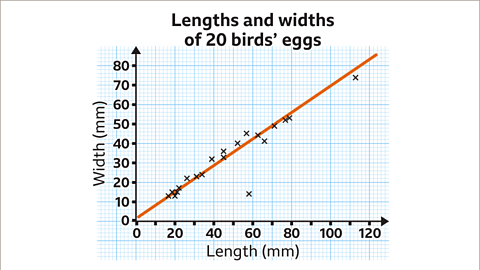
Image caption, The line of best fit should be a straight line which approximates the trend. The line is drawn as close as possible to all the data points, once any outliers have been identified. It does not have to go through every data point. It does not have to go through the origin.
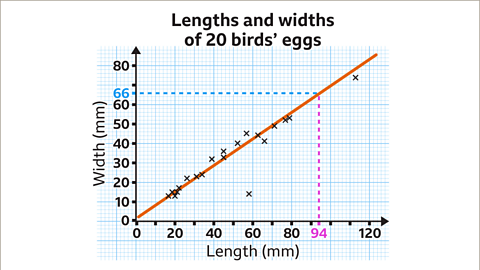
Image caption, The line of best fit can be used to make predictions. For example, an egg of length 94 mm would have an expected width of 66 mm.
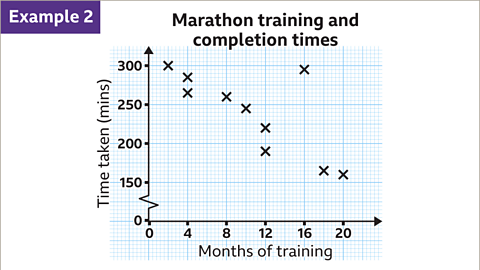
Image caption, The scatter diagram shows the relationship between the months a competitor trained for and the time it took them to complete a marathon. The graph shows a negative correlation. The vertical scale is going up in increments of 50. Between each multiple of 50 are ten subdivisions. Each subdivision is worth 5 minutes.
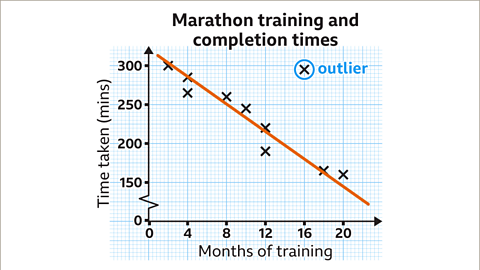
Image caption, One piece of data does not match the trend. It is a long way from the line of best fit. This outlier is at (16, 295).

Image caption, The line of best fit approximates the trend. It can be used to predict a competitor with a completion time of 180 minutes has trained for 16 months.
1 of 6
Question
The scatter graph shows the relationship between the temperature on a given day and the number of ice creams sold in a café.
A line of best fit has been drawn.
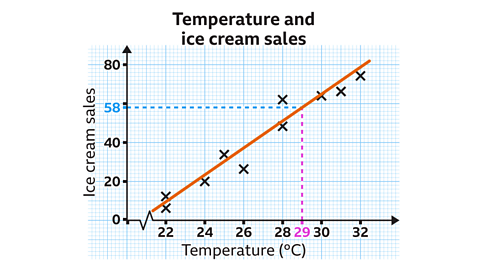
Use the line of best fit to predict how many ice creams will be sold on a day where the temperature is 29°C.
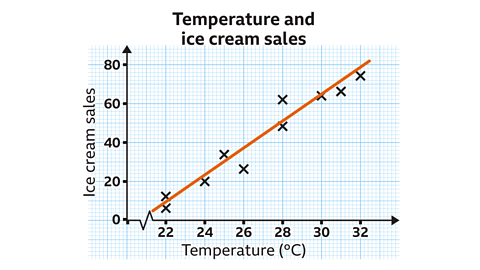
The vertical scale is going up in increments of 20
Between each multiple of 20 are ten subdivisions. Each subdivision is worth two ice creams.
Using the line of best fit, 58 ice creams would be sold when the temperature is 29°C.
Practise understanding scatter diagrams
Quiz
Practise understanding scatter diagrams with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

A data analystA person whose job is to collect, study and explain data in order to solve problems or make informed decisions. may use scatter diagrams to look for patterns and trends. These can then be used to make projections. A projection is an estimate or guess at what may happen in the future based on trends.
However, there is no guarantee that a linear trendA steady increase or decrease of variables over time. On a graph this would look like a straight line going upwards or downwards. will continue indefinitely. For example, as a person's age increases during childhood, their height typically increases. This would be a positive correlationThe relationship between two sets of data. Usually described as positive or negative.. This trend does not continue forever as, although people continue to grow older, they eventually stop growing taller.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from BBC Bitesize.

More on Representing data
Find out more by working through a topic
- count1 of 6

- count2 of 6
- count3 of 6
- count4 of 6